ERQUAF
Over the past fifteen years, the paradigm of quantum entanglement has revolutionised the understanding of strongly correlated lattice systems. Entanglement and closely related concepts originating from quantum information theory are optimally suited for quantifying and characterising quantum correlations and have therefore proven instrumental for the classification of the exotic phases discovered in condensed quantum matter. One groundbreaking development originating from this research is a novel class of variational many body wave functions known as tensor network states. Their explicit local structure and unique entanglement features make them very flexible and extremely powerful both as a numerical simulation method and as a theoretical tool.
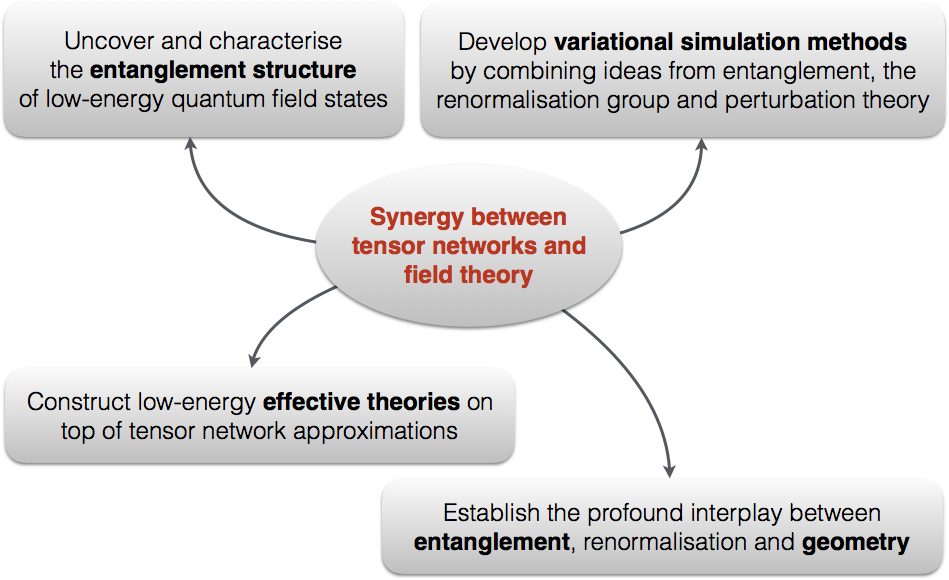
ERQUAF is the acronym of the ERC project that sets as its goal to lift this “entanglement methodology” into the realm of quantum field theory. Indeed, in high energy physics, the widespread interest in entanglement has only been triggered recently, due to the intriguing connections between entanglement and the structure of spacetime that arise in black hole physics and quantum gravity. Furthermore, direct continuum limits of various tensor network ansätze have been formulated over the past few years. However, the application thereof is largely unexplored territory and holds promising potential.
Establishing the synergy between field theory and entanglement theory is the central theme of ERQUAF, and a number of goals are set out in the following graph.
Tangential research projects
Aside from my commitment to ERQUAF, I am also involved in a number of tangential projects.
-
Tensor networks for topological order, classification of phases, phase transitions, fermions, …
-
Tensor network algorithms for quenches, thermalisation, …
-
Software packages and experiments to implement tensor network algorithms in Julia; look here.