Hoofdstuk 7 - Functieruimten

Author

Jutho Haegeman

Published

December 6, 2024

Doel van dit hoofdstuk

Inzicht krijgen in de complicaties van het werken met functieruimten
Orthonormale basissen voor functieruimten:
- orthogonale veeltermen:
  - belangrijkste eigenschappen
  - voornaamste families die relevant zijn in de fysica
- Fourierreeks:
  - eigenschappen
  - convergentiesnelheid
  - verband met discrete Fouriertransformatie

Doel van dit hoofdstuk

Belangrijkste operatoren op functieruimten:

integraaloperatoren, multiplicatie-operatoren, differentiaaloperatoren
Eigenschappen van onbegrensde operatoren
- Toegevoegde van onbegrensde operator
- Verschil tussen symmetrisch en zelftoegevoegd
- Belang hiervan in de context van differentiaaloperatoren en randvoorwaarden
Intuitie krijgen voor de spectraaltheorie van begrensde en onbegrensde operatoren op oneindig-dimensionale Hilbertruimten aan de hand van relevante voorbeelden

Functieruimten en normen

(geen stellingen of bewijzen)

Functieruimten

Gegeven een vectorruimte $Y$ over ${\mathbb{F}}$ en een willekeurige verzameling $X$:

verzameling $X^Y$ van functies $f:Y \to X$ vormt een vectorruimte over ${\mathbb{F}}$, waarbij de lineaire structuur gewoon puntsgewijs wordt gedefinieerd m.b.v. deze van $Y$:

\[(a f + b g)(x) = a f(x) + b g(x), \forall x \in X\]

Voorbeelden:

$Y = {\mathbb{F}}$, $X = \{1,\ldots,n\}$: $Y^X \cong {\mathbb{F}}^n$
$Y = {\mathbb{F}}$, $X = {\mathbb{N}}_0$: vectorruimte van oneindig lange rijen

$\rightarrow$ functieruimte wordt typisch gebruikt in de context waar $X$ onaftelbaar is:

$X = [a,b]$, $X = {\mathbb{R}}$, $X = \Omega \subseteq {\mathbb{R}}^d$

$\rightarrow$ bijkomende eigenschappen: continuïteit, kwadratische integreerbaarheid, …

belangrijk dat deze compatibel zijn met (behouden blijven onder) lineaire combinaties

Lebesgue-ruimten

We willen ook graag minstens een norm (vanaf sectie 7.2: inwendig product):

\[f:X \to Y \quad \rightarrow \quad{\left\lVert f\right\rVert}_p = \left(\int_{X} {\left\lVert f(x)\right\rVert}_Y^p \,{\mathrm{d}}x\right)^{1/p} \quad ?\]

$Y$ moet zelf reeds een norm hebben:

vanaf nu $Y = {\mathbb{F}}$: ${\left\lVert f(x)\right\rVert}_Y = {\left\lvert f(x)\right\rvert}$ (voor de eenvoud, veralgemening triviaal)
We hebben een concept van integreren over $X$ nodig $\Rightarrow$ bijkomende complicaties
- $X$ voldoende regulier: vanaf nu $X = [a,b]\subseteq {\mathbb{R}}$ of $X = {\mathbb{R}}$ (voor de eenvoud)
- de functie $f$ moet “integreerbaar” zijn binnen het gebruikte integraalconcept
- de integraal mag niet divergeren
- de integraal moet voldoen aan driehoeksongelijkheid
- de integraal kan nul worden voor functies die niet de nul-functie zijn

$\rightarrow$ beperken tot deelverzameling van functies: moet deelruimte zijn!

Lebesgue-ruimten

$\mathcal{L}^p(I,{\mathbb{F}})$ is de verzameling van functies $f:I\to {\mathbb{F}}$ (met dus $I=[a,b]$ of $I = {\mathbb{R}}$) die integreerbaar zijn en waarvoor $\int_I {\left\lvert f(x)\right\rvert}^p \,{\mathrm{d}}x$ eindig is

preciese definitie hangt af van integraalconcept (zie verder)
als $f$ integreerbaar is, is ${\left\lvert f\right\rvert}^p$ integreerbaar
het geval $p=\infty$ laten we voorlopig buiten beschouwing
$\mathcal{L}^p(I,{\mathbb{F}})$ vormt een vectorruimte (lineaire combinaties van twee integreerbare functies is integreerbaar, integraal van ${\left\lvert a f(x) + b g(x)\right\rvert}^p$ can begrensd worden met behulp van convexiteit van ${\left\lvert\cdot\right\rvert}^p$
resulterende definitie ${\left\lVert f\right\rVert}_p = \left(\int_I {\left\lvert f(x)\right\rvert}^p \,{\mathrm{d}}x\right)^{1/p}$ voldoet aan driehoeksongelijkheid (Minkowski)
${\left\lVert f\right\rVert}_p$ is niet positief definiet, er zijn niet-triviale functies waarvoor ${\left\lVert f\right\rVert}_p = 0$

$\Rightarrow$ seminorm

Van seminorm naar norm

Observatie 1:voor $f,g \in \mathcal{L}^p(I,{\mathbb{F}})$

${\left\lVert f\right\rVert}_p = 0$ en ${\left\lVert g\right\rVert}_p = 0$ $\Rightarrow {\left\lVert a f + b g\right\rVert}_p = 0$

(wegens driehoeksongelijkheid en absolute homogeniteit)

$\Rightarrow$ verzameling $U = \{f | {\left\lVert f\right\rVert}_p = 0\}$ vormt deelruimte van $\mathcal{L}^p(I,{\mathbb{F}})$
functies waarvoor ${\left\lVert f - g\right\rVert}_{p} = 0 \Leftrightarrow f-g \in U$ noemen we “bijna overal” gelijk; dit is een equivalentierelatie

$\rightarrow$ $L^p(I,{\mathbb{F}}) = \mathcal{L}^p(I,{\mathbb{F}})/U$: de vectorruimte van equivalentieklassen van functies die bijna overal gelijk zijn

(in de praktijk werken we nog steeds gewoon met functies, die dan representatief zijn voor alle andere functies binnen die equivalentieklasse)

Van seminorm naar norm

Observatie 2: voor $f,g \in \mathcal{L}^p(I,{\mathbb{F}})$

${\left\lVert f - g\right\rVert}_{p} = 0$ $\Rightarrow {\left\lVert f\right\rVert}_p = {\left\lVert g\right\rVert}_p$

(wegens ${\left\lvert{\left\lVert f\right\rVert}-{\left\lVert g\right\rVert}\right\rvert} \leq {\left\lVert f - g\right\rVert}$, eveneens uit driehoeksongelijkheid)
${\left\lVert f\right\rVert}_p$ neemt voor alle functies binnen een equivalentieklasse dezelfde waarde aan
met elk element uit $L^p(I,{\mathbb{F}})$ kan een eenduidige waarde ${\left\lVert f\right\rVert}_p$ worden geassocieerd (onafhankelijk van de keuze $f$ binnen de klasse)
Op $L^p(I,{\mathbb{F}})$ is ${\left\lVert\cdot\right\rVert}_p$ een norm
Is $L^p(I,{\mathbb{F}})$ metrisch compleet (Banachruimte) ?
- deze vraag ereist dat we integralen en limieten kunnen omdraaien, e.g.:
  
  \[\lim_{n\to \infty} \int_I {\left\lvert f_n(x)\right\rvert}^p\,{\mathrm{d}}x = \int_I {\left\lvert\lim_{n\to\infty} f_n(x)\right\rvert}^p\,{\mathrm{d}}x = \int_I \lim_{n\to\infty} {\left\lvert f_n(x)\right\rvert}^p\,{\mathrm{d}}x \quad ?\]
- tegenvoorbeeld: $f_n(x) = 2n^2 \exp(-n^2 x^2)$
  
  $\Rightarrow$: $f_n \to 0$ terwijl $\int_0^1 f_n(x)\,{\mathrm{d}}x = 1 - \exp(-n^2) \to 1$

Lebesgue-integraal

Riemann-integraal $\int_a^b f(x)\,{\mathrm{d}}x$:
- partitie $P$ van $[a,b]$: $\Delta_k = [x_{k-1},x_k]$ met $a = x_0 < x_1 < \ldots < x_{n_1} < x_n=b$
- $m_k = \inf_{x \in \Delta_k} f(x)$ en $M_k = \sup_{x \in \Delta_k} f(x)$:
  
  $s_{f,P} = \sum_{k=1}^{n} m_k (x_k - x_{k-1})$ en $S_{f,P} = \sum_{k=1}^{n} M_k (x_k - x_{k-1})$
- integraal bestaat als $s_f = \sup_{P} s_{f,P} = \inf_{P} S_{f,P} = S_f$
  
  (functies met “niet te veel” discontinuïteiten)
werkt niet voor bvb $\chi_{\mathbb{Q}}(x) = \begin{cases} 1,& x \in {\mathbb{Q}}\\ 0,& x \in {\mathbb{R}}\setminus {\mathbb{Q}}\end{cases}$ (Dirichlet functie)
- Voorwaarden voor het omdraaien van limieten en integralen met Riemann-integraal zijn heel streng
- Er zijn rijen van integraarbare functies waarvoor de limiet bestaat maar niet (Riemann)-integreerbaar is

Lebesgue-integraal

Lebesgue-integraal $\int_a^b f(x)\,{\mathrm{d}}x$: eerst voor $0 \leq f(x) \leq M$
- partitie van $[0,M]$: $0 = y_0 < y_1 < \ldots < y_{n-1} < y_n = M$
- invers beeld (pre-image) $E_k = f^{-1}([y_{k-1},y_k))$
- $l_{f,P} = \sum_{k=1}^{n} y_{k-1} \mu(E_k)$ en $L_{f,P} = \sum_{k=1}^{n} y_k \mu(E_k)$
  
  met $\mu(E_k)$ de “grootte” (maat) van $E_k$

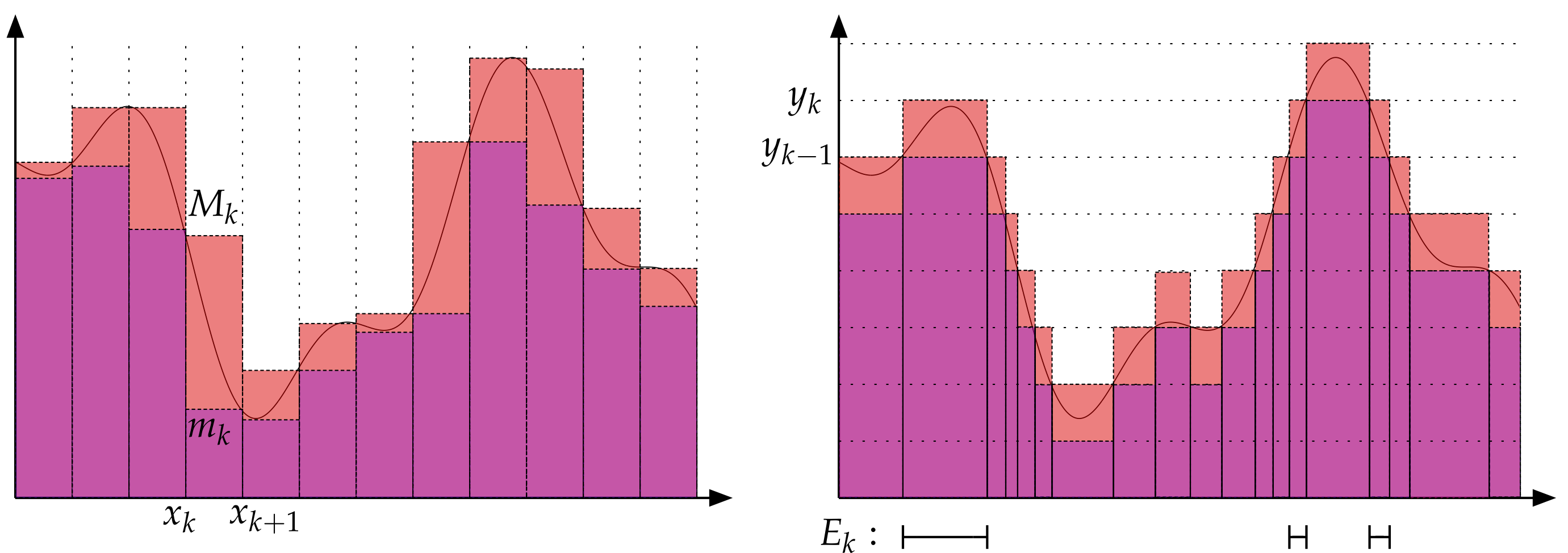
Lebesgue-integraal

Probleem zit verdoken in de maat $\mu(E_k)$:

$E_k$ is niet noodzakelijk een interval; meer algemene deelverzameling van ${\mathbb{R}}$

We willen graag:
- $\mu([a,b]) = \mu([a,b)) = \mu((a,b]) = \mu((a,b)) = b - a$ ($\forall a < b \in {\mathbb{R}}$)
- $\mu\left(\bigcup\{A_i, i= 1,2,\ldots\}\right) = \sum_{i} \mu(A_i)$ voor disjuncte verzamelingen $A_i$ (countable additivity)
$\Rightarrow$ een $\mu$ met deze eigenschappen kan niet worden gedefinieerd voor de collectie $\mathcal{P}({\mathbb{R}})$ van alle mogelijke deelverzamelingen van ${\mathbb{R}}$ (of van een interval binnen ${\mathbb{R}}$)

$\Rightarrow$ de definitie van $\mu$ wordt beperkt tot een subcollectie van toegelaten deelverzamelingen van ${\mathbb{R}}$

$\Rightarrow$ een functie is Lebesgue-integreerbaar als alle inverse beelden $E_k = f^{-1}([y_{k-1},y_k))$ van dit toegelaten type zijn

$\Rightarrow$ een functie die Riemann-integreerbaar is, is Lebesgue-integreerbaar en de integralen hebben dezelfde waarde

“Lebesgue integralen verhouden zich tot Riemann integralen zoals ${\mathbb{R}}$ tot ${\mathbb{Q}}$”

“Bijna overal” en “maat nul” (nulverzamelingen)

Een positieve functie $f$ heeft $\int_I f(x)\,{\mathrm{d}}x = 0$ enkel als de verzameling $N=\{x | f(x)>0\}$ maat nul heeft: $\mu(N) = 0$
Nulverzamelingen: verzamelingen $N$ met $\mu(N)=0$
- Individueel punt
- Aftelbaar eindig aantal punten
- Ook onaftelbare verzamelingen kunnen maat nul hebben
Andere “bijna overal” definities:
- functies $f$ en $g$ zijn bijna overal gelijk, als er een verzameling $N$ bestaat met $\mu(N)=0$ zodat $f(x)=g(x)$ voor alle $x \in I \setminus N$
- $\lim_{n \to \infty} f_n$ convergeert “bijna overal” puntsgewijs naar $f$, als er een verzameling $N$ bestaat met $\mu(N)=0$ zodat $\lim_{n \to \infty} f_n(x) = f(x)$ voor alle $x \in I \setminus N$

Compleetheid van $L^p(I;{\mathbb{F}})$

Ten opzichte van de Lebesgue-integraal zijn er stellingen die garanderen dat, voor een rij $(f_n)$ die “bijna overal” puntsgewijs convergeert naar $f$,

$\lim_{n\to \infty} \int_I f_n(x)\,{\mathrm{d}}x = \int_I \lim_{n\to\infty} f_n(x)\,{\mathrm{d}}x$ als

$\forall n \in {\mathbb{N}}_0$: $f_n(x) \leq f_{n+1}(x)$ “bijna overal”

of

$\forall n \in {\mathbb{N}}_0$: ${\left\lvert f_n(x)\right\rvert} \leq g(x)$ “bijna overal” voor een integreerbare functie $g$
deze resultaten kunnen worden gebruikt om aan te tonen dat

$L^p(I,{\mathbb{F}})$ is Banachruimte (stelling van Riesz-Fischer)
uitbreidingen:
- voor $p=\infty$: $L^\infty(I,{\mathbb{F}})$ gedefinieerd via ${\left\lVert f\right\rVert}_\infty = \mathrm{ess}\ \sup_{x\in I} {\left\lvert f\right\rvert} = \inf\big\{M \geq 0 |\ \mu\left(\{x \in I | {\left\lvert f(x)\right\rvert}> M\right\}) = 0\big\}$
- $L^p_w(I,{\mathbb{F}})$ met norm ${\left\lVert f\right\rVert}_{p,w} = \left(\int_{I} w(x) {\left\lvert f(x)\right\rvert}^p \,{\mathrm{d}}x\right)^{1/p}$ voor integreerbare functie $w$ met $w(x)>0$ voor alle $x \in I$

Bijkomende opmeringen

$I = [a,b]$ (compact): $L^p(I,{\mathbb{F}}) {\preccurlyeq}L^q(I,{\mathbb{F}})$ als $p > q$

$I = {\mathbb{R}}$: $L^p(I,{\mathbb{F}})$ en $L^q(I,{\mathbb{F}})$ hebben elk elementen die de andere niet bevat
Interessante dichte deelruimtes als $I$ compact:
- polynomen
- continue functies $C^0(I,{\mathbb{F}})$, gladde functies $C^\infty(I,{\mathbb{F}})$, elke $C^k(I,{\mathbb{F}})$ voor $k \in {\mathbb{N}}$
$\Rightarrow \overline{C^k(I,{\mathbb{F}})} = L^p(I,{\mathbb{F}})$: sluiting hangt af van definitie limiet en dus van ${\left\lVert\cdot\right\rVert}_p$
Interessante dichte deelruimtes als $I = {\mathbb{R}}$:
- $C_c^k(I,{\mathbb{F}})$: continu (afleidbare) functies met compacte “drager” (support)
  
  $\rightarrow$ $\mathrm{supp}(f) = \overline{\{ x \in I |\ f(x) \neq 0\}} \subseteq I$
$L^p(I,{\mathbb{F}})$ is “separabel”: laat aftelbare fundamentele verzameling $S$ toe

(verzameling waarvoor geldt dat $\overline{{\mathbb{F}}S} = L^p(I,{\mathbb{F}})$, niet noodzakelijk een basis)
- $I$ compact: $S=\{x^k,k\in{\mathbb{N}}\}$, $S=\{\exp({\mathrm{i}}\frac{2\pi}{L} k x), k \in{\mathbb{Z}}\}$,
- $I = {\mathbb{R}}$: $S=\{x^n \chi_{[-N,N]}, n \in {\mathbb{N}}, N \in {\mathbb{N}}\}$

Hilbertruimten en inwendig product

$L^2(I,{\mathbb{F}})$ is een Hilbertruimte: ${\left\lVert\cdot\right\rVert}_2$ voldoet aan parallellogramregel en is afkomstig van het inwendig product

\[{\left\langle f,g\right\rangle} = \int_I \overline{f(x)}g(x)\,{\mathrm{d}}x\]
$L_w^2(I,{\mathbb{F}})$ is een Hilbertruimte: ${\left\lVert\cdot\right\rVert}_{2,w}$ voldoet aan parallellogramregel en is afkomstig van het inwendig product

\[{\left\langle f,g\right\rangle}_w = \int_I w(x) \overline{f(x)}g(x)\,{\mathrm{d}}x\]

met dus $w(x) > 0$ voor $x \in I$ (op nulverzameling na)
nog algemener: ${\left\langle f,g\right\rangle} = \iint_I w(x,y) \overline{f(x)}g(y)\,{\mathrm{d}}x{\mathrm{d}}y$ ?

$\rightarrow$ weinig gebruikt, precieze voorwaarden op $w(x,y)$ niet duidelijk

Orthogonale veeltermen

$\{x^n, n\in{\mathbb{N}}_0\}$ is een fundamentele verzameling voor:
- $L^2([a,b], {\mathbb{F}})$
- $L^2_w(I, {\mathbb{F}})$ voor $I = {\mathbb{R}}$ of $I = {\mathbb{R}}_{\geq 0}$ in combinatie met goed gekozen $w$
$\{x^n, n\in{\mathbb{N}}_0\}$ kan omgevormd worden tot een basis door de equivalente orthogonale/orthonormale rij te vormen via het Gram-Schmidt algoritme (en dan het expansietheoriem toe te passen)
Verschillende families van orthogonale polynomen (door keuzes van $I$ en $w$)

Orthogonale veeltermen

Gram-Schmidt algoritme toegepast op $\{x^n, n\in{\mathbb{N}}_0\}$ $\Rightarrow$ $\{p_n(x), n \in {\mathbb{N}}_0\}$ met

$p_n(x)$ is een polynoom van graad $n$ met reële coëfficiënten
- volgt uit structuur Gram-Schmidt
- $p_n(x)$ is orthogonaal op alle met polynomen van graad $<n$
- niet steeds genormaliseerd: ${\left\langle p_n,p_m\right\rangle}_w \sim C_n \delta_{n,m}$
- voor symmetrisch interval en $w(x)=w(-x)$:
  
  $p_n$ bevat enkel even (oneven) machten van $x$ voor $n$ even (oneven)
$x p_n(x) = a_{n} p_{n+1}(x) + b_n p_{n}(x) + c_{n} p_{n-1}(x)$ (bewijs aan bord)

met $c_0 = 0$ en $c_{n} {\left\langle p_{n-1},p_{n-1}\right\rangle}_w = a_{n-1} {\left\langle p_n,p_n\right\rangle}_w$ $\Rightarrow c_n = a_{n-1}$
- vermenigvuldigen met $x$ heeft tridiagonale “matrixrepresentatie” t.o.v. basis $p_n$
- als normalisatie van basis $n$-onafhankelijk:
  
  $c_n = a_{n-1} \Leftrightarrow$ symmetrische matrixrepresentatie

Orthogonale veeltermen

Orthogonale projector op deelruimte van polynomen van graad $n$:

\[({\hat{P}}_n f)(x) = \int_I w(y) K_n(x,y) f(y)\,{\mathrm{d}}y = \int_I w(y) \left[\sum_{k=0}^{n} \frac{p_k(x) p_k(y)}{{\left\langle p_k,p_k\right\rangle}_w} \right] f(y)\,{\mathrm{d}}y\]

met hierin (Christoffel-Darboux formule): \[\sum_{k=0}^{n} \frac{p_k(x) p_k(y)}{{\left\langle p_k,p_k\right\rangle}_w} = \begin{cases} \frac{a_n}{{\left\langle p_n,p_n\right\rangle}_w} \frac{ p_{n+1}(x) p_n(y) - p_{n}(x) p_{n+1}(y)}{x-y},& x \neq y\\ \frac{a_n}{{\left\langle p_n,p_n\right\rangle}_w} ( p_{n+1}'(x) p_n(y) - p_{n}'(x) p_{n+1}(y)),& x = y \end{cases}\]

(bewijs aan bord)
$p_n$ heeft $n$ verschillende nulpunten in $I$;

de nulpunten van $p_n$ liggen tussen deze van $p_{n+1}$ in (alternerend)

(bewijs aan bord)

Orthogonale veeltermen: Legendre

$I = [-1,+1]$, $w(x)=1$:

\[\begin{equation} \begin{split} &P_0(x) = 1,\quad P_1(x) = x,\quad P_2(x) = \frac{1}{2}(3 x^2 - 1),\\ &P_3(x) = \frac{1}{2}(5x^3-3x),\quad P_4(x) = \frac{1}{8}(35 x^4 - 30x^2 + 3), \quad \ldots \end{split} \end{equation}\]
Genererende functie (Legendre 1782): $\frac{1}{\sqrt{1 - 2x t + t^2}} = \sum_{n=0}^{+\infty} P_n(x) t^n$

$\rightarrow$ nuttig om eigenschappen aan te tonen:
- uit $\int_{-1}^{+1} \frac{1}{\sqrt{1 - 2x t + t^2}} \frac{1}{\sqrt{1 - 2x s + s^2}} \,{\mathrm{d}}x = \sum_{n,m=0}^{+\infty} {\left\langle P_n,P_m\right\rangle} t^n s^m = \frac{1}{\sqrt{ts}} \log \frac{1 + \sqrt{ts}}{1 - \sqrt{ts}}$
  
  $\Rightarrow {\left\langle P_n,P_m\right\rangle} = \int_{-1}^{+1} P_n(x) P_m(x) \,{\mathrm{d}}x = \frac{2}{2n +1} \delta_{n,m}$
- uit afgeleide naar $t$ $\rightarrow$ Bonnet recursieformule:
  
  $(n+1) P_{n+1}(x) + n P_{n-1}(x) = (2n+1) x P_n(x)$
- Rodrigues formule: $P_n(x) = \frac{1}{2^n n!} \frac{{\mathrm{d}}^n\ }{{\mathrm{d}}x^n} (x^2 -1)^n$

Orthogonale veeltermen: Hermite

$I = {\mathbb{R}}$, $w(x)=\exp(-x^2)$: (polynomen worden kwadratisch integreerbaar)

\[\begin{equation} \begin{split} &H_0(x) = 1,\quad H_1(x) = 2x,\quad H_2(x) = 4 x^2 - 2,\\ &H_3(x) = 8x^3-12x,\quad H_4(x) = 16 x^4 - 48x^2 + 12, \quad \ldots \end{split} \end{equation}\]
Genererende functie: $\exp( 2 x t - t^2) = \sum_{n=0}^{+\infty} \frac{1}{n!} H_n(x) t^n$

$\rightarrow$ nuttig om eigenschappen aan te tonen:
- uit $\int_{-\infty}^{+\infty} {\mathrm{e}}^{-x^2} {\mathrm{e}}^{2x s - s^2} {\mathrm{e}}^{2x s - s^2}\,{\mathrm{d}}x = \sum_{m,n=0}^{+\infty} \frac{{\left\langle H_m,H_n\right\rangle}_w}{m! n!} s^m t^n = \sqrt{\pi} {\mathrm{e}}^{2 s t}$
  
  $\Rightarrow {\left\langle H_m,H_n\right\rangle}_w = \int_{-\infty}^{+\infty} {\mathrm{e}}^{-x^2} H_m(x) H_n(x)\,{\mathrm{d}}x = 2^n n! \sqrt{\pi} \delta_{m,n}$
- uit afgeleide naar $t$ $\rightarrow$ Bonnet recursieformule:
  
  $H_{n+1}(x) + 2n H_{n-1}(x) = 2 x H_{n}(x)$
- Rodrigues formule: $H_n(x) = (-1)^n {\mathrm{e}}^{x^2} \frac{{\mathrm{d}}^n}{{\mathrm{d}}x^n} {\mathrm{e}}^{-x^2}$
$\{\phi_n(x) \sim H_n(x) {\mathrm{e}}^{-\frac{x^2}{2}},n \in {\mathbb{N}}\}$

is orthogonale fundamentele verzameling (basis) voor $L^2({\mathbb{R}},{\mathbb{F}})$

Orthogonale veeltermen: Laguerre

$I = [0,+\infty)$, $w(x)=\exp(-x)$:

\[\begin{equation} \begin{split} &L_0(x) = 1,\quad L_1(x) = 1-x,\quad L_2(x) = \frac{1}{2}(x^2 - 4x + 2),\\ &L_3(x) = \frac{1}{6}(-x^3 + 9x^2 - 18 x +6)\quad \ldots \end{split} \end{equation}\]
Genererende functie: $\frac{1}{1-t} \exp\left(-x\frac{ t}{1 - t}\right) = \sum_{n=0}^{+\infty} L_n(x) t^n$

$\rightarrow$ nuttig om eigenschappen aan te tonen:
- uit $\int_{0}^{+\infty} {\mathrm{e}}^{-x} \frac{1}{1-s} \exp\left(\frac{-x s}{1 - s}\right)\frac{1}{1-t} \exp\left(\frac{-x t}{1 - t}\right)\,{\mathrm{d}}x = \sum_{m,n=0}^{+\infty} {\left\langle L_m,L_n\right\rangle}_w s^mt^n = \frac{1}{1-ts}$
  
  $\Rightarrow {\left\langle L_m,L_n\right\rangle}_w = \int_0^{+\infty} {\mathrm{e}}^{-x} L_m(x) L_n(x) \,{\mathrm{d}}x = \delta_{m,n}$
- uit afgeleide naar $t$ $\rightarrow$ Bonnet recursieformule:
  
  $(n+1) L_{n+1}(x) + n L_{n-1}(x) = (2n + 1 - x) L_n(x)$
- Rodrigues formule: $L_n(x) = \frac{{\mathrm{e}}^x}{n!} \frac{{\mathrm{d}}^n\ }{{\mathrm{d}}x^n} (x^n {\mathrm{e}}^{-x})$

Orthogonale veeltermen: Chebyshev

$I = [-1,1]$, $w(x) = (1-x^2)^{-1/2}$:

\[\begin{equation} \begin{split} &T_0(x) = 1,\quad T_1(x) = x,\quad T_2(x) = 2x^2-1,\quad T_3(x) = 4x^3 - 3x,\quad \ldots \end{split} \end{equation}\]
Genererende functie: $\frac{1- x t}{1 - 2x t+ t^2} = \sum_{n=0}^{+\infty} T_n(x) t^n$
In dit geval: ${\left\langle f,g\right\rangle}_w = \int_{-1}^{+1} \frac{1}{\sqrt{1-x^2}} f(x) g(x)\,{\mathrm{d}}x = \int_{0}^{+\pi} f(\cos \theta) g(\cos \theta) \,{\mathrm{d}}\theta$
- $T_n(x) = T_n(\cos \theta) = \cos(n \theta) = \cos(n \arccos x)$
- \[\begin{align*} {\left\langle T_m,T_n\right\rangle}_w = \int_{-1}^{+1} \frac{T_m(x) T_n(x)}{\sqrt{1-x^2}} \,{\mathrm{d}}x = \int_0^{+\pi} \cos(m\theta)\cos(n\theta)\,{\mathrm{d}}\theta = \begin{cases} \pi, & m = n = 0\\ \frac{\pi}{2} \delta_{n,m}, &\text{otherwise}\end{cases} \end{align*}\]
- $T_{n\pm 1}(\cos \theta) = \cos(\theta) \cos(n \theta) \mp \sin(\theta) \sin(n\theta)$:
  
  recursierelatie $T_{n+1}(x) = 2x T_n(x) - T_{n-1}(x)$

$\rightarrow$ vooral in numerieke analyse, statistiek, minder in fysica

Toepassing: Gaussische kwadratuur

Numerieke benadering van integraal op basis van functiewaarden op een discrete, eindige verzameling $\{x_i \in I; i=1,\ldots,n\}$:

\[\int_I w(x) f(x)\,{\mathrm{d}}x \approx \sum_{i=1}^{n} a^i f(x_i)\]

$\rightarrow$ moet lineaire functionaal zijn van de functiewaarden $\{f(x_i)\}$
met $n$ punten: benadering exact voor veeltermen van graad $\leq n-1$

\[\begin{equation} \begin{bmatrix} 1 & 1 & 1 & \dots & 1\\ x_1 & x_2 & x_3 & \dots & x_n\\ (x_1)^2 & (x_2)^2 & (x_3)^2 & \dots & (x_n)^2\\ \vdots & & & \ddots & \vdots\\ (x_1)^{n-1} & (x_2)^{n-1} & (x_3)^{n-1} & \dots & (x_n)^{n-1} \end{bmatrix} \begin{bmatrix} a^1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n} \end{bmatrix} = \begin{bmatrix} b^0\\ b^1 \\ b^2 \\ \vdots \\ b^{n-1} \end{bmatrix} \end{equation}\]

met $b^k = \int_I w(x) x^k\,{\mathrm{d}}x$: lineair systeem met Vandermonde matrix

Toepassing: Gaussische kwadratuur

Kunnen we beter doen als we de $\{x_i\}$ slim kiezen?

Kunnnen we de benadering exact maken voor veeltermen tot graad $\leq 2n-1$ ?
Moeilijk niet-lineair probleem?

Gauss: kies $\{x_i; i=1,\ldots,n\}$ als nulpunten van de orthogonale veelterm $p_n$ geassocieerd aan $I$ en $w$
- we kiezen $a^i$ zodat exact voor veeltermen tot graad $n-1$
- $\int w(x) p_n(x) q(x)\,{\mathrm{d}}x = 0$ voor elke $q$ van graad $\leq n-1$
  
  $\rightarrow$ benaderingsformule correct als $p_n(x_i) =0$ voor elke $x_i$
- willekeurige polynoom van graad $\leq 2n-1$:
  
  $f(x) = p_n(x) q(x) + r(x)$ met $r(x)$ veelterm met graad $\leq n-1$
  
  $\Rightarrow \int w(x) f(x)\,{\mathrm{d}}x = \int w(x) r(x)\,{\mathrm{d}}x = \sum a^i r(x_i) = \sum a^i f(x_i)$
Vandermonde-matrix inverteren is numeriek instabiel: eigenschappen van orthogonale veeltermen kunnen ook helpen om $a^i$ te vinden

$\rightarrow$: niet te kennen

Fourierreeksen

Periodieke functies

periodieke functies $f:{\mathbb{R}}\to {\mathbb{C}}$ met $f(x+L) = f(x)$
- functiewaarden $x \in [0,L)$ $\to$ periodiek uitbreiden
- functie op circel $\cong$ 1-dimensionale torus ${\mathbb{T}}^1 = {\mathbb{R}}/(L{\mathbb{Z}})$.
trigonometische veelterm van graad $n$:

\[\begin{align} f(x) &= \frac{a_0}{2} + \sum_{k=1}^{n} a_k \cos\left(\frac{2\pi}{L} k x\right) + \sum_{k=1}^n b_k \sin\left(\frac{2\pi}{L} k x\right)= \sum_{k=-n}^{+n} c_k \exp\left({\mathrm{i}}\frac{2\pi}{L} k x\right) \end{align}\]
- $a_k = c_k + c_{-k}$ voor $k \in {\mathbb{N}}$ en $b_k = {\mathrm{i}}(c_k - c_{-k})$ voor $k\in {\mathbb{N}}_0$
- orthonormale basis: $S=\left\{ \varphi_k(x) = \frac{1}{\sqrt{L}} {\mathrm{e}}^{+{\mathrm{i}}\frac{2\pi}{L} k x};\ k =-n,-n+1,\dots,0,\dots, n-1, n\right\}$
meerdimensionale Fourier-basis ($\boldsymbol{x} \in \mathbb{T}^d = L_1 \times L_2 \times \cdots \times L_d$):

\[\left\{\varphi_{\boldsymbol{k}}(\boldsymbol{x}) = \frac{1}{(L_1 L_2 \dots L_d)^{1/2}} {\mathrm{e}}^{+{\mathrm{i}}(\frac{2\pi}{L_1} k_1 x_1 + \dots + \frac{2\pi}{L_d} k_d x_d)}; \boldsymbol{k} \in {\mathbb{Z}}^d\right\}\]

Trigonometrische veeltermen en Fouriercoefficiënten

Fouriercoefficiënten: $\widehat{f}_k = {\left\langle\varphi_k,f\right\rangle} = \frac{1}{\sqrt{L}} \int_{0}^{L} f(x) {\mathrm{e}}^{-{\mathrm{i}}\frac{2\pi}{L} k x}\,{\mathrm{d}}x$ ($\forall k \in {\mathbb{Z}}$)
Orthogonale projector op trigonometrische veeltermen van graad $n$:

\[\begin{align} f_n(x) = ({\hat{P}}_n f)(x) &= \sum_{k=-n}^{+n} {\left\langle\varphi_k,f\right\rangle} \varphi_k(x)= \sum_{k=-n}^{+n} \widehat{f}_k \varphi_k(x) = \frac{1}{\sqrt{L}} \sum_{k=-n}^{+n} \widehat{f}_k {\mathrm{e}}^{+{\mathrm{i}}\frac{2\pi}{L} k x} \\ &= \sum_{k=-n}^{+n} \frac{1}{L} \int_0^L f(t) {\mathrm{e}}^{+ {\mathrm{i}}\frac{2\pi}{L} k (x - t)}\,{\mathrm{d}}t = \int_0^L D_n(x-t) f(t)\,{\mathrm{d}}t\label{eq:function:fourierapproximationn} \end{align}\]

met $D_n(x) = \frac{1}{L} \sum_{k=-n}^{+n} {\mathrm{e}}^{+ {\mathrm{i}}\frac{2\pi}{L} k x} = \frac{\sin\left(\frac{(2n+1)\pi}{L}x\right)}{L \sin\left(\frac{\pi}{L}x\right)}$ (Dirichlet kernel)
Fourierreeks: \[\lim_{n \to \infty} \frac{1}{\sqrt{L}} \sum_{k=-n}^{+n} \widehat{f}_k {\mathrm{e}}^{+{\mathrm{i}}\frac{2\pi}{L} k x}\]

Fouriercoefficiënten: eigenschappen

\[\widehat{f}_k = {\left\langle\varphi_k,f\right\rangle} = \frac{1}{\sqrt{L}} \int_{0}^{L} f(x) {\mathrm{e}}^{-{\mathrm{i}}\frac{2\pi}{L}k x}\,{\mathrm{d}}x\]

Bestaan ($\forall k \in {\mathbb{Z}}$) voor elke $f \in L^1([0,L];{\mathbb{C}})$ met ${\left\lvert\widehat{f}_k\right\rvert} \leq \frac{1}{\sqrt{L}} {\left\lVert f\right\rVert}_1 \Rightarrow {\left\lVert\widehat{f}\right\rVert}_{\infty} = \sup_{k \in {\mathbb{Z}}} {\left\lvert\widehat{f}\right\rvert}_{\infty} \leq \frac{1}{\sqrt{L}}{\left\lVert f\right\rVert}_1$
Lineariteit: $h(x) = a f(x) + b g(x) \implies \widehat{h}_k = a \widehat{f}_k + b \widehat{g}_k$
Translatie (in ruimte/tijd): $h(x) = f(x-x_0) \implies \widehat{h}_k = {\mathrm{e}}^{-{\mathrm{i}}\frac{2\pi}{L}k x_0} \widehat{f}_k$
Modulatie (verschuiging in frequentie): $h(x) = f(x) {\mathrm{e}}^{{\mathrm{i}}\frac{2\pi}{L} k_0 x} \implies \widehat{h}_k = \widehat{f}_{k-k_0}$
Conjugatie: $h(x) = \overline{f(x)} \implies \widehat{h}_k = \overline{\widehat{f}_{-k}}$
Tijd-/frequentie-omkering: $h(x) = f(-x) \implies \widehat{h}_k = \widehat{f}_{-k}$
(Discrete) herschaling: $h(x) = f(s x) \implies \widehat{h}_{k} = \begin{cases} \frac{1}{s}\widehat{f}_{k/s} ,&\text{$k$ is veelvoud van $s$}\\ 0,&\text{anders}\end{cases},\quad\forall s \in {\mathbb{N}}_0$

Convoluties

Convolutie van periodieke functies:

\[\begin{align}(f \ast g)(x) &= \int_0^L f(x-y \mod L) g(y)\,{\mathrm{d}}y \\ &= \int_0^L f(y) g(x-y \mod L)\,{\mathrm{d}}y = (g \ast f)(x) \end{align}\]
- opnieuw periodieke functie
- voor $f,g \in L^1([0,L])$ is $f\ast g \in L^1([0,L])$ (aan bord)
Fouriercoefficiënten:

$h(x) = (f \ast g)(x) = \int_0^L f(x-y \mod L) g(y)\,{\mathrm{d}}y \implies \widehat{h}_k = \sqrt{L} \widehat{f}_k \widehat{g}_k$

Convergentie (geen stellingen/bewijzen)

Beschouw $f_n = \frac{1}{\sqrt{L}} \sum_{k=-n}^{+n} \widehat{f}_k {\mathrm{e}}^{+{\mathrm{i}}\frac{2\pi}{L} k x}$
De Fourierbasis is een fundamentele verzameling in $L^1([0,L],{\mathbb{F}})$:

er bestaat een rij $(\tilde{f}_n)$ van trigonometrische veeltermen zodat

\[\lim_{n\to \infty} {\left\lVert\tilde{f}_n - f\right\rVert}_1 = 0\]

voor alle $f \in L^1([0,L],{\mathbb{F}})$ (concreet: $\tilde{f}_n = \frac{f_0 + f_1+f_2+\ldots+f_n}{n+1}$).
Wat zegt dit over $\lim_{n\to \infty} {\left\lVert f_n - f\right\rVert}_2$ ?
- bemerk dat $L^2([0,L],{\mathbb{F}}) {\preccurlyeq}L^1([0,L],{\mathbb{F}})$
- maar ${\left\lVert\cdot \right\rVert}_2$ is strengere maat van convergentie
- $L^2([0,L],{\mathbb{F}})$ kan geen niet-triviale functies bevatten die loodrecht staan op alle Fourier/trigonometrische polynomen
$\rightarrow$ expansiestelling: $\lim_{n\to \infty} {\left\lVert f_n - f\right\rVert}_2=0$

$\implies \sum_{k \in {\mathbb{Z}}} {\left\lvert\widehat{f}_k\right\rvert}^2 = {\left\lVert\widehat{f}\right\rVert}_2^2$ en dus voor grote $k$: ${\left\lvert\widehat{f}_k\right\rvert}$ daalt sneller dan ${\left\lvert k\right\rvert}^{-1/2}$

Gladheid en convergentiesnelheid

Een periodieke functie is continu, i.e. $f \in C^({\mathbb{T}}^1_L)$, als \[\begin{align*} f(x) &= \lim_{y \to x} f(y), \forall x \in (0,L),&\text{and}&&\lim_{y \stackrel{>}{\to} 0} f(y) &= \lim_{y \stackrel{<}{\to} L} f(y). \end{align*}\]
$f \in C^p({\mathbb{T}}^1_L)$: $h(x) = f^{(p)}(x)\implies \widehat{h}_k = \left({\mathrm{i}}\frac{2\pi}{L} k\right)^p \widehat{f}_k$ (bewijs via partiële integratie)
Convergentiesnelheid voor uniforme convergentie: ${\left\lVert f_n - f\right\rVert}_\infty \leq \sqrt{\frac{2}{L(2p-1)}} \frac{1}{n^{p-1/2}} \left[\sum_{k \in {\mathbb{Z}}} {\left\lvert k\right\rvert}^{2p} {\left\lvert\widehat{f}_k\right\rvert}^2\right]^{1/2}$ (zonder bewijs)

voor willekeurige $p > 1/2$
- als Fourierreeks uniform convergeert, is limiet continu
- enkel mogelijk als $f$ continu is: noodzakelijk maar niet voldoende
- als $f' \in L^2([0,L],{\mathbb{F}}) \implies \sum_{k\in {\mathbb{Z}}} {\left\lvert k\right\rvert}^2{\left\lvert\widehat{f}_k\right\rvert}^2 = \left(\frac{L}{2\pi}\right)^2 {\left\lVert f'\right\rVert}_2^2 < \infty$
  
  $\implies$ Fourierreeks voor $f$ convergeert uniform

Convoluties herbekeken

convolutie $h = f \ast g \leftrightarrow \widehat{h}_k = \sqrt{L} \widehat{f}_k \ast \widehat{g}_k$
- $f, g \in L^2([0,L],{\mathbb{F}}) \implies {\left\lvert\widehat{f}_k\right\rvert}$, ${\left\lvert\widehat{g}_k\right\rvert} < {\left\lvert k\right\rvert}^{-1/2}$ $\implies {\left\lvert\widehat{h}_k\right\rvert} < {\left\lvert k\right\rvert}^{-1}$
  
  $\Rightarrow$ $h=f \ast g$ heeft uniform convergerende Fourierreeks (en is dus continu)
omgekeerde resultaat?
- discrete convolutie: $\widehat{h}_k = (\widehat{f}\ast \widehat{g})_k=\sum_{l\in {\mathbb{Z}}} \widehat{f}_{k-l} \widehat{g}_l = \sum_{l\in {\mathbb{Z}}} \widehat{f}_{l} \widehat{g}_{k-l} = (\widehat{g}\ast \widehat{f})_k$
- $h(x) = f(x) g(x)\implies \widehat{h}_k =\frac{1}{\sqrt{L}} (\widehat{f} \ast \widehat{g})_k = \frac{1}{\sqrt{L}} \sum_{\ell \in {\mathbb{Z}}} \widehat{f}_{k-l} \widehat{g}_l$
  
  onder welke voorwaarden? niet te kennen
absoluut sommeerbare rijen: $\widehat{f} \in \ell^1({\mathbb{Z}},{\mathbb{C}})$: $\sum_{k\in{\mathbb{Z}}} {\left\lvert\widehat{f}_k\right\rvert} < \infty$
- $\widehat{f}\in \ell^1({\mathbb{Z}})$ $\implies$ Fourierreeks convergeert absoluut $\implies$ Fourierreeks convergeert uniform $\implies f$ continu
- $\widehat{f},\widehat{g} \in \ell^1({\mathbb{Z}}) \implies \widehat{f}\ast \widehat{g} \in \ell^1({\mathbb{Z}})$
  
  continuïteit van $f$ en $g$ noodzakelijk maar niet voldoende

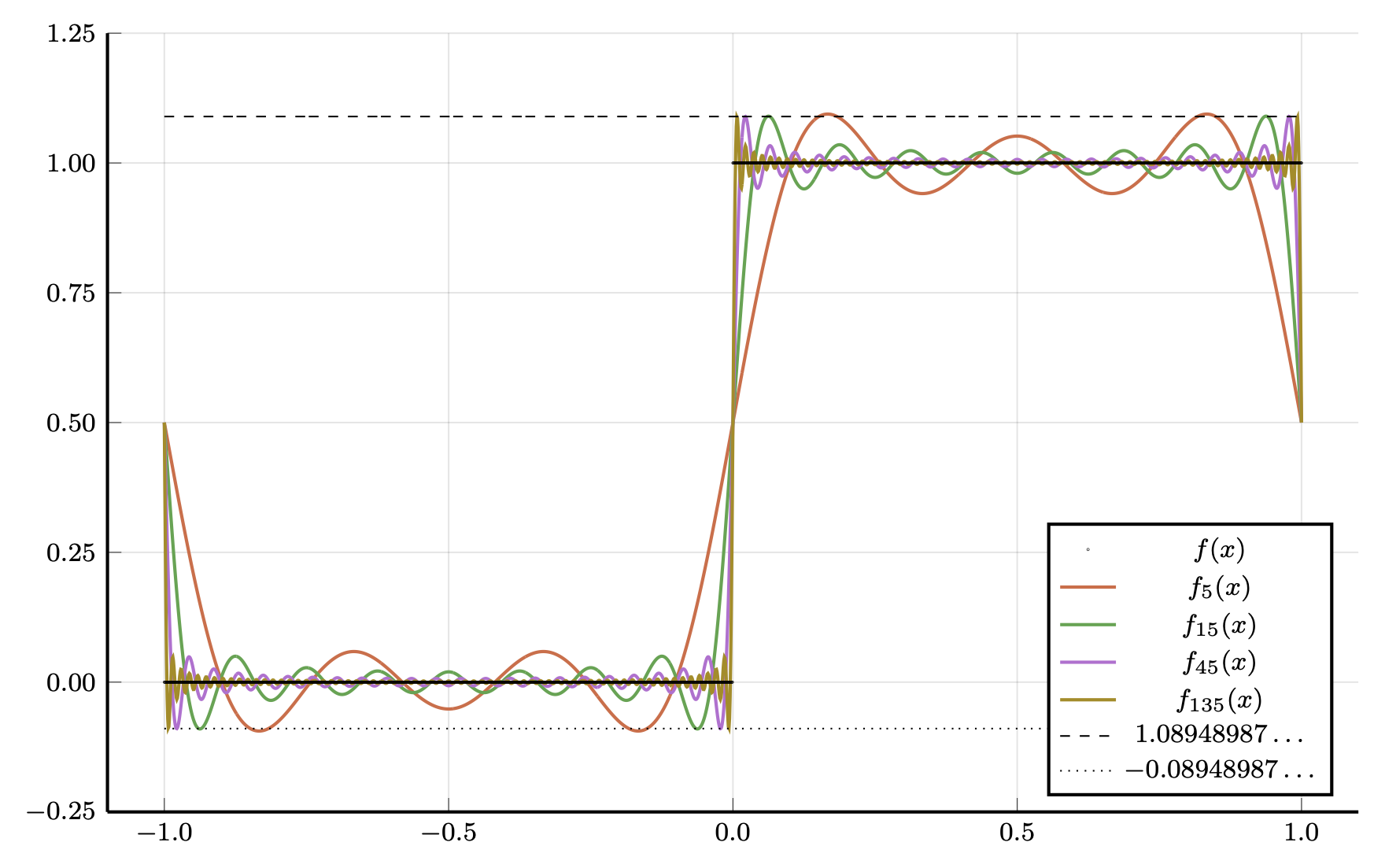
Stuksgewijze continuïteit en Gibbsfenoneem

$f(x) = H(x) = \frac{1}{2}(1 + \mathop{\mathrm{sgn}}(x))$ op interval $[-L/2,+L/2]$
\[\begin{align*} \widehat{f}_k =\begin{cases} \frac{\sqrt{L}}{2},&k=0\\\frac{{\mathrm{i}}\sqrt{L}}{2\pi} \frac{\cos\left(\pi k\right)-1}{k},&k \neq 0 \end{cases} = \begin{cases} \frac{\sqrt{L}}{2}\delta_{k,0},&\text{$k$ even}\\ \frac{-{\mathrm{i}}\sqrt{L}}{\pi} \frac{1}{k},&\text{$k$ odd} \end{cases} \end{align*}\]
${\left\lvert\widehat{f}_k\right\rvert} \sim {\left\lvert k\right\rvert}^{-1}$: geen absolute of uniforme convergentie $\Leftrightarrow$ niet continu
$f_{2m+1}(x) = \frac{1}{\sqrt{L}}\sum_{{\left\lvert k\right\rvert}\leq 2m+1} \widehat{f}_k {\mathrm{e}}^{+{\mathrm{i}}\frac{2\pi}{L} k x}$ $= \frac{1}{2}+\frac{2}{\pi} \left[ \sin\left(\frac{2\pi}{L} x\right) + \frac{1}{3} \sin\left(\frac{6\pi}{L} x\right) + \frac{1}{5} \sin\left(\frac{10\pi}{L} x\right) + \dots \right]$
- $f_{2m+1}(0) = 1/2 \Rightarrow \lim_{n\to \infty} f_n(0) = 1/2 = (f(0^-)+f(0^+))/2$
- $f_{2m}\left(\frac{L}{4m}\right) = \frac{1}{2} + \frac{2}{\pi} \sum_{l=0}^{m-1} \frac{\sin\left(\pi \frac{2l+1}{2m}\right)}{(2l+1)} = \frac{1}{2} + \frac{1}{\pi}\left(\frac{\pi}{m}\right) \sum_{l=0}^{m-1} \frac{\sin\left(\pi \frac{2l+1}{2m}\right)}{\pi \frac{2l+1}{2m}}$
  
  $\qquad \stackrel{m\to\infty}{\longrightarrow} \frac{1}{2} + \frac{1}{\pi} \int_0^\pi \frac{\sin(x)}{x}\,{\mathrm{d}}x$

Stuksgewijze continuïteit en Gibbsfenoneem

Gibbsfenomeen: functie met discontinuïteit $f(x_0^{\pm}) = f_0 \pm \frac{1}{2} a$
- $\lim_{n\to\infty} f_n(x_0) = f_0$
- $\lim_{n \to \infty} f_n\left(x_0 \pm \frac{L}{2n} \right) = f_0 \pm \frac{a}{\pi} \int_0^{\pi} \frac{\sin(x)}{x}\,{\mathrm{d}}x = f(x_0)^\pm \pm a \left[\frac{1}{\pi} \int_0^{\pi} \frac{\sin(x)}{x}\,{\mathrm{d}}x - \frac{1}{2}\right]$ $\qquad= f(x_0)^\pm \pm a \cdot (0.089489872236\dots)$

Relatie met discrete Fouriertransformatie

$f(x) = \frac{1}{\sqrt{L}} \sum_{k \in {\mathbb{Z}}}\widehat{f}_k {\mathrm{e}}^{+{\mathrm{i}}\frac{2\pi}{L} k x}.$
‘Bemonster’ (sample) $f$:

$f_j = f(x_j)$ met $x_j = j \epsilon$; $j=0,1,\dots, N-1$ en $N=L/\epsilon$
Discrete Fouriertransformatie van ‘samples’ \[\begin{align} F^k &= \frac{1}{\sqrt{N}} \sum_{j = 0}^{N-1} f_j {\mathrm{e}}^{-{\mathrm{i}}\frac{2\pi}{N} k j} =\frac{1}{\sqrt{N}} \frac{1}{\sqrt{L}} \sum_{j=0}^{N-1} \left(\sum_{l \in {\mathbb{Z}}} \widehat{f}_l {\mathrm{e}}^{+{\mathrm{i}}\frac{2\pi}{L} l j \epsilon}\right) {\mathrm{e}}^{-{\mathrm{i}}\frac{2\pi}{N} k j}\nonumber \\ & = \frac{\sqrt{\epsilon}}{N} \sum_{l \in {\mathbb{Z}}} \widehat{f}_l \sum_{j=0}^{N-1} {\mathrm{e}}^{{\mathrm{i}}\frac{2\pi}{N} j (l-k)} = \sqrt{\epsilon} \sum_{p \in {\mathbb{Z}}} \widehat{f}_{k + p N}. \end{align}\]
Snel dalende Fouriercoefficiënten: $F^k = \widehat{f}_{\min(k, k-N)} + \dots$
Fouriercoefficiënten exact begrensd: $\widehat{f}_k = 0$ voor ${\left\lvert k\right\rvert}>n$ $\Leftrightarrow$ $f$ is trigonometrische veelterm van graad $n$

$\Rightarrow$ exacte reconstructie mogelijk uit samples als $\epsilon \leq L/(2n+1)$

Operatoren op Hilbertruimten

Veelvoorkomende operatoren op functieruimten

Hilbertuimte $H = L^2(I,{\mathbb{C}})$: lineaire afbeeldingen $f \mapsto g$ met $f,g \in H$

Integraaloperatoren: \[g(x) = ({\hat{A}}f)(x) = \int_I A(x,y) f(y) \,{\mathrm{d}}y\]
- $A:I \times I \to {\mathbb{C}}$: (integraal)kern van de ‘integraaltransformatie’
- meest directe veralgemening van een matrix ${\mathsf{A}}$ en $w^i = A^i_{\ j} v^j$
Vermenigvuldigingsoperatoren: \[g(x) = ({\hat{M}}_h f)(x) = h(x) f(x)\]
- belangrijkste voorbeeld: “positie-operator” ${\hat{X}}$
  
  $\rightarrow$ ${\hat{M}}_h = h({\hat{X}})$
- vergelijkbaar met diagonaalmatrices
  
  $\rightarrow$ ${\hat{M}}_h$ als integraaloperator met $A(x,y) = h(x)\delta(x-y)$ ? (zie later)

Veelvoorkomende operatoren op functieruimten

Differentiaaloperatoren:
- bekendste voorbeeld: $g(x) = ({\hat{D}}f)(x) = f'(x)$
- vaak geschreven als ${\hat{P}} = -{\mathrm{i}}{\hat{D}}$ (momentum-operator)
- andere differentiaaloperatoren: $p({\hat{D}})$ met $p$ een veelterm
Identiteitsoperator: $g(x) = ({\hat{1}}f)(x) = f(x)$
- resolutie van de identiteit t.o.v. orthonormale basis:
  
  \[f(x) = \sum_{n =0}^{+\infty} {\left\langle\varphi_n,f\right\rangle} \varphi_n(x) = \int_I \sum_{n=0}^{+\infty} \varphi_n(x) \overline{\varphi_n(y)} f(y)\,{\mathrm{d}}y\]
  
  $\rightarrow$ neemt de vorm aan van integraaloperator met kern
  
  \[A(x,y) = \sum_{n=0}^{+\infty} \varphi_n(x) \overline{\varphi_n(y)}\]
  
  $\Rightarrow A(x,y) = \delta(x-y)$ ? (zie later)

Domein van een operator

Sommige operatoren hebben niet de volledige Hilbertruimte als domein:
- ${\hat{D}}$ kan enkel op afleidbare functies werken
- ${\hat{M}}_h f$ is mogelijks niet meer kwadratisch integreerbaar
$\rightarrow$ domein is deel~~verzameling~~ruimte van $H$
beschouw operator ${\hat{A}}$ met domein $\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}} {\preccurlyeq}H$:
- als ${\hat{A}}$ begrensd $\Rightarrow$ continu $\Rightarrow$ actie van ${\hat{A}}$ ook gedefinieerd op $\overline{\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}}$
- als $\overline{\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}} \neq H$, definieer actie op ${v}\in \overline{\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}}^\perp$ als ${\hat{A}}({v}) = {o}$
$\Rightarrow$ voor begrensde operatoren: $\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}$ kan altijd gelijk worden gekozen aan $H$

$\Rightarrow$ voor onbegrensde operatoren: operatoren waarvan het domein $\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}$ dicht is in $V$, maar geen uitbreiding naar randpunten mogelijk wegens gebrek aan continuïteit
- bijvoorbeeld: (continu) afleidbare functies zijn dicht in $L^2(I)$
  
  $\rightarrow$ kies $\mathop{\mathrm{\mathcal{D}}}_{{\hat{D}}} = C^1(I,{\mathbb{F}})$

Domein van een operator

Vanaf nu: $\mathop{\mathrm{End}}(H)$ = verzameling van alle lineaire afbeeldingen van een dichte deelruimte van $H$ naar $H$ (“densily defined”)
${\hat{A}},{\hat{B}} \in \mathop{\mathrm{End}}(V)$ met domein $\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}, \mathop{\mathrm{\mathcal{D}}}_{{\hat{B}}}$:
- beeld/bereik $\mathcal{R}_{{\hat{A}}} = \mathop{\mathrm{im}}({\hat{A}}) = \{ {\hat{A}}{v}| {v}\in \mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}\}$
- gelijkheid: ${\hat{A}} = {\hat{B}} \iff \mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}} = \mathop{\mathrm{\mathcal{D}}}_{{\hat{B}}}$ en ${\hat{A}}{v}= {\hat{B}} {v}$ voor alle ${v}\in \mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}$
- restrictie/extensie: ${\hat{A}} \subset {\hat{B}} \iff \mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}} {\preccurlyeq}\mathop{\mathrm{\mathcal{D}}}_{{\hat{B}}}$ en ${\hat{A}}{v}= {\hat{B}} {v}$ voor alle ${v}\in \mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}$
  
  $\rightarrow$ ${\hat{B}}$ is een extensie van ${\hat{A}}$, ${\hat{A}}$ is een restrictie van ${\hat{B}}$
$\Rightarrow$ een (onbegrensde) operator is gedefinieerd door zijn actie EN zijn domein!
- als fysici denken we meestal niet na over domein
- behalve voor afleidingsoperatoren: randvoorwaarden (zie later)

Begrensde en onbegrensde operatoren

Integraaloperator:

${\left\lVert{\hat{A}}f\right\rVert}^2 = \int_I \underbrace{{\left\lvert\int_I A(x,y) f(y)\,{\mathrm{d}}y\right\rvert}^2}_{\Downarrow\ \text{Cauchy-Schwarz}} \,{\mathrm{d}}x$ $\quad\leq \int_I \left(\int_I {\left\lvert A(x,y)\right\rvert}^2\,{\mathrm{d}}y\right)^2 \left(\int_I f(y),{\mathrm{d}}y\right)^2\,{\mathrm{d}}x = \left(\int_I\int_I {\left\lvert A(x,y)\right\rvert}^2 \,{\mathrm{d}}y{\mathrm{d}}x\right) {\left\lVert f\right\rVert}^2$

$\Rightarrow$ begrensd als $\left(\int_I\int_I {\left\lvert A(x,y)\right\rvert}^2 \,{\mathrm{d}}y{\mathrm{d}}x\right) < \infty$
Vermenigvuldigingsoperator:

\[{\left\lVert{\hat{M}}_h f\right\rVert}^2 = \int_I {\left\lvert h(x) f(x)\right\rvert}^2\,{\mathrm{d}}x \leq \left(\mathrm{ess}\ \sup_{x \in I} {\left\lvert h(x)\right\rvert}^2\right) {\left\lVert f\right\rVert}^2\]

$\Rightarrow$ positie-operator ${\hat{X}}$ op $L^2(I,{\mathbb{F}})$ is begrensd als $I$ begrensd domein is, maar is onbegrensd op $L^2({\mathbb{R}},{\mathbb{F}})$

Begrensde en onbegrensde operatoren

Afleidingsoperator: altijd onbegrensd
- op $L^2([0,L],{\mathbb{C}})$: $f_k = \frac{1}{\sqrt{L}} \exp({\mathrm{i}}\frac{2\pi}{L}k x)$
  
  $\rightarrow$ ${\left\lVert f_k\right\rVert}_2 = 1$ en ${\left\lVert{\hat{D}}f_k\right\rVert}_2 = \frac{2\pi}{L} {\left\lvert k\right\rvert}$ voor arbitraire $k \in {\mathbb{Z}}$
- op $L^2({\mathbb{R}},{\mathbb{C}})$:
$f_n(x) = \begin{cases} \sin(\frac{2\pi}{L}n x),&x \in [0,L]\\ 0,& x \not\in [0,L] \end{cases}$

$\rightarrow ({\hat{D}}f_n)(x) = f'_n(x) = \begin{cases} \frac{2\pi}{L} n \cos(\frac{2\pi}{L}n x),&x \in [0,L]\\ 0,& x \not\in [0,L]\end{cases}$

$\rightarrow {\left\lVert f_n\right\rVert}_2 = \frac{L}{2}$ en ${\left\lVert f'_n\right\rVert}_2 = \pi n$ voor arbitraire $n \in {\mathbb{N}}_0$

Begrensde en onbegrensde operatoren

$[{\hat{A}},{\hat{B}}] = {\hat{1}}$ (of technisch: restrictie $\subset {\hat{1}}$):

$\Rightarrow$ minstens 1 van beide operatoren is onbegrensd (bewijs aan bord)
Voorbeeld 1: $(({\hat{D}}{\hat{X}} - {\hat{X}} {\hat{D}}) f)(x) = \frac{{\mathrm{d}}\ }{{\mathrm{d}}x} \big(x f(x)\big) - x \frac{{\mathrm{d}}\ }{{\mathrm{d}}x} f(x) = f(x)$

$\rightarrow$ ${\hat{D}}$ altijd onbegrensd, ${\hat{X}}$ afhankelijk van $I$ in $L^2(I,{\mathbb{F}})$
Voorbeeld 2: $H = \ell^2({\mathbb{N}})$: rijen ${v}=(v_0,v_1,v_2,\ldots)$ met $\sum_{n \in {\mathbb{N}}} {\left\lvert{v}_n\right\rvert}^2 < \infty$
- dichte deelruimten:
  - rijen waarvoor $\sum_{n \in {\mathbb{N}}} n^p {\left\lvert{v}_n\right\rvert}^2 < \infty$
  - rijen met een eindig aantal niet-nulelementen
- \[\begin{align} {\hat{A}}^- {e}_n &= \begin{cases} {o}, & n=0\\ \sqrt{n} {e}_{n-1},&n > 0 \end{cases}, &{\hat{A}}^+{e}_{n} = \sqrt{n+1} {e}_{n+1}.\label{eq:function:annihilationcreation} \end{align}\]
- ${\left[{\hat{A}}^-,{\hat{A}}^+\right]} {e}_n = {e}_n$
  
  (beide onbegrensd; domein $\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}^\pm} = \{{v}\in \ell^2({\mathbb{N}}) | \sum_{n \in {\mathbb{N}}} n {\left\lvert{v}_n\right\rvert}^2 < \infty\}$)

Toegevoegde van een onbegrensde operator

Definitie van toegevoegde operator: mogelijke problemen
- ${v}\mapsto {\left\langle{w},{\hat{A}}{v}\right\rangle}$ is niet langer een continue lineaire functionaal op $H$
- ${\hat{A}}^\dagger$ waarschijnlijk onbegrensd: welk domein?
Constructie van de toegevoegde van een onbegrensde operator
1. definieer domein: $\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}^\dagger}$ bevat alle ${w}\in H$ zodat ${v}\mapsto {\left\langle{w},{\hat{A}}{v}\right\rangle}$ een begrensde $\leftrightarrow$ continue lineaire functionaal is voor alle ${v}\in \mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}$
2. aangezien $\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}$ een dichte deelruimte is van $H$, kan de actie van ${v}\mapsto {\left\langle{w},{\hat{A}}{v}\right\rangle}$ nu uitgebreid worden naar volledig $H$ (maar niet de actie van ${\hat{A}}$ zelf)
3. nu kunnen we Riesz representatie-theorema toepassen om aan ${w}$ een nieuwe vector ${\hat{A}}^\dagger({w})$ te associeren zodat
\[{\left\langle{w},{\hat{A}}{v}\right\rangle} = {\left\langle{\hat{A}}^\dagger{w},{v}\right\rangle},\forall {v}\in \mathop{\mathrm{\mathcal{D}}}\,\!_{{\hat{A}}}, {w}\in \mathop{\mathrm{\mathcal{D}}}\,\!_{{\hat{A}}^\dagger}\]
1. uniciteit, lineairiteit van ${\hat{A}}^\dagger$ en andere eigenschappen volgen zoals gewoonlijk

Toegevoegde: eigenschappen en voorbeelden

Voorbeeld 1: ${\left\langle{w},{\hat{A}}^-{v}\right\rangle} = \sum_{n \in {\mathbb{N}}} \sqrt{n+1} \overline{w^n} v^{n+1} = {\left\langle{\hat{A}}^+{w},{v}\right\rangle}$ voor alle ${v},{w}$ met $\sum_{n \in {\mathbb{N}}} n {\left\lvert v_n\right\rvert}^2 < \infty$ $\Rightarrow {\hat{A}}^+ = ({\hat{A}}^-)^\dagger$: domein van deze operatoren is reeds maximaal
Voorbeeld 2: op $L^2([a,b],{\mathbb{F}})$, beschouw ${\hat{D}}$ met als domein alle afleidbare functies met $f' \in L^2([a,b],{\mathbb{F}})$ en $f(a)=f(b)=0$

\[\int_a^b \overline{g(x)} f'(x)\,{\mathrm{d}}x = g(b)f(b) - g(a)f(a) - \int_a^b \overline{g'(x)}f(x)\,{\mathrm{d}}x\]

$\Rightarrow$ $({\hat{D}}^\dagger g)(x) = -g'(x)$ met als domein alle afleidbare functies $g$ met $g' \in L^2([a,b],{\mathbb{F}})$, zonder bijkomende randvoorwaarden
${\hat{A}} \subset {\hat{B}} \Rightarrow {\hat{B}}^\dagger \subset {\hat{A}}^\dagger$ (minder ${v}\in \mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}$ dan in $\mathop{\mathrm{\mathcal{D}}}_{{\hat{B}}} \implies$ meer ${w}\in \mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}^\dagger}$ mogelijk)
Als ${\hat{A}}^\dagger$ zelf ook dicht gedefineerd is, dan kunnen we ${\hat{A}}^{\dagger\dagger}$ definiëren:

$\rightarrow$ ${\hat{A}} \subset {\hat{A}}^{\dagger\dagger}$ ($\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}^{\dagger\dagger}}$ bevat alle ${v}$ zodat ${w}\mapsto {\left\langle{v},{\hat{A}}^\dagger{w}\right\rangle} = {\overline{{\left\langle{\hat{A}}^\dagger {w},{v}\right\rangle}}}$ continu is voor alle ${w}\in \mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}^\dagger}$: zeker voldaan ${v}\in \mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}$)

Symmetrische en zelftoegevoegde operatoren

symmetrische / hermitische / hermitisch symmetrische operator: \[{\left\langle{w},{\hat{A}}{v}\right\rangle} = {\left\langle{\hat{A}}{w},{v}\right\rangle}, \forall {v},{w}\in \mathop{\mathrm{\mathcal{D}}}\,\!_{{\hat{A}}}\]

(symmetrisch wordt ook gebruikt in complexe geval)
zelftoegevoegde operatoren:

\[{\hat{A}}^\dagger = {\hat{A}} \Leftrightarrow \mathop{\mathrm{\mathcal{D}}}\,\!_{{\hat{A}}^\dagger}=\mathop{\mathrm{\mathcal{D}}}\,\!_{{\hat{A}}}\ \text{en}\ {\hat{A}}{v}= {\hat{A}}^\dagger{v},\forall {v}\in \mathop{\mathrm{\mathcal{D}}}\,\!_{{\hat{A}}}\]

(zelftoegevoegd $\Rightarrow$ symmetrisch)
symmetrische operator:

$\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}{\preccurlyeq}\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}^\dagger}$ en ${\hat{A}}^\dagger {v}= {\hat{A}}{v}$ voor alle ${v}\in \mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}$

\[\Rightarrow {\hat{A}} \subset {\hat{A}}^\dagger \Rightarrow {\hat{A}}^{\dagger\dagger} \subset {\hat{A}}^\dagger\] \[\Rightarrow {\hat{A}} \subset {\hat{A}}^{\dagger\dagger} \subset {\hat{A}}^\dagger\]

Uitgebreid voorbeeld

Beschouw de operator ${\hat{P}}$ met actie $({\hat{P}}f)(x)=-{\mathrm{i}}f'(x)$ en de identiteit \[\begin{align*} {\left\langle g,{\hat{P}} f\right\rangle} &= \int_{a}^{b} \overline{g(x)} (-{\mathrm{i}}) f'(x)\,{\mathrm{d}}x = -{\mathrm{i}}\left[\overline{g(b)}f(b) - \overline{g(a)} f(a)\right] + \int_{a}^{b} \overline{(-{\mathrm{i}}) g'(x)}f(x)\,{\mathrm{d}}x\nonumber\\ &= -{\mathrm{i}}\left[\overline{g(b)}f(b) - \overline{g(a)} f(a)\right] + {\left\langle{\hat{P}} g,f\right\rangle} \end{align*}\]

We moeten het domein nog specifiëren:

${\hat{P}}_1$ met domein $\mathop{\mathrm{\mathcal{D}}}_1 = \{f \in L^2([a,b]) | \text{$f'$ bestaat en $f' \in L^2([a,b])$}\}$
- niet symmetrisch
- $\mathop{\mathrm{\mathcal{D}}}_{{\hat{P}}_1^\dagger} = \{f \in \mathop{\mathrm{\mathcal{D}}}_1 | f(a) = f(b) = 0\}$
${\hat{P}}_2$ met domein $\mathop{\mathrm{\mathcal{D}}}_2 = \{f \in \mathop{\mathrm{\mathcal{D}}}_1 | f(a) = f(b) = 0\}$
- symmetrisch
- ${\hat{P}}_2^\dagger = {\hat{P}}_1$: ${\hat{P}}_2 \subset {\hat{P}}_1$
- ${\hat{P}}_2^{\dagger\dagger} = {\hat{P}}_1^\dagger = {\hat{P}}_2$

Uitgebreid voorbeeld

We moeten het domein nog specifiëren:

${\hat{P}}_1$ met domein $\mathop{\mathrm{\mathcal{D}}}_1 = \{f \in L^2([a,b]) | \text{$f'$ bestaat en $f' \in L^2([a,b])$}\}$
- niet symmetrisch
- $\mathop{\mathrm{\mathcal{D}}}_{{\hat{P}}_1^\dagger} = \{f \in \mathop{\mathrm{\mathcal{D}}}_1 | f(a) = f(b) = 0\}$
Stel bijvoorbeeld ${\hat{P}}_4$ met $\mathop{\mathrm{\mathcal{D}}}_4 = \{f \in C^1([a,b]) | f(a) = f(b) = 0\}$
- nog steeds symmetrisch
- nog steeds ${\hat{P}}_4^\dagger = {\hat{P}}_1$
- ${\hat{P}}_4^{\dagger\dagger} = {\hat{P}}_2$ $\Rightarrow$ ${\hat{P}}_4 \subset {\hat{P}}_4^{\dagger\dagger} \subset {\hat{P}}_4^\dagger$

Uitgebreid voorbeeld

Kunnen we een extensie vinden van ${\hat{P}}_2$ waarvoor ${\hat{P}}_3 = {\hat{P}}_3^\dagger$ ?

Stel ${\hat{P}}_3$ met $\mathop{\mathrm{\mathcal{D}}}_3 =\{f \in \mathop{\mathrm{\mathcal{D}}}_1 | f(b) = {\mathrm{e}}^s f(a)\}$ voor een $s \in {\mathbb{C}}$
- er geldt inderdaad $\mathop{\mathrm{\mathcal{D}}}_2 {\preccurlyeq}\mathop{\mathrm{\mathcal{D}}}_3 {\preccurlyeq}\mathop{\mathrm{\mathcal{D}}}_1$
- symmetrisch? als $-{\mathrm{i}}[{\mathrm{e}}^{\overline{s}+s} - 1] \overline{g(a)}f(a) = 0 \Rightarrow$ $s$ zuiver imaginair
- toegevoegde operator? $\mathop{\mathrm{\mathcal{D}}}_{{\hat{P}}_3^\dagger} = \{g \in \mathop{\mathrm{\mathcal{D}}}_1 | g(b) = {\mathrm{e}}^{-{\overline{s}}} g(a)\}$
$\Rightarrow$ voor ${\mathrm{e}}^s = {\mathrm{e}}^{{\mathrm{i}}\theta}$ (voor een $\theta \in [0,2\pi)$): zelf-toegevoegd (en dus symmetrisch)
- “verdraaide (twisted) randvoorwaarden”
  
  omvat periodiek ($\theta=0$, $f(a)=f(b)$) en antiperiodiek ($\theta=\pi$, $f(b)=-f(a)$)
Belang: eigenwaarden en eigenvectoren
- ${\hat{P}}_1$: ${\mathrm{e}}^{i \lambda x}$ is een eigenvector met eigenwaarde $\lambda$ voor alle $\lambda \in {\mathbb{C}}$
- ${\hat{P}}_2$: geen eigenvectoren of eigenwaarden
- ${\hat{P}}_3$: eigenvectoren $\varphi_k(x) = \frac{1}{\sqrt{L}} {\mathrm{e}}^{{\mathrm{i}}\frac{2\pi}{L} \left(k + \frac{\theta}{2\pi}\right) x}$ met eigenwaarden $\lambda_k = \frac{2\pi}{L} \left(k + \frac{\theta}{2\pi}\right)$ voor alle $k \in {\mathbb{Z}}$

Positie- en momentumoperator op $L^2({\mathbb{R}})$

Zonder bewijs: op $H=L^2({\mathbb{R}})$ zijn ${\hat{X}}$ en ${\hat{P}}$ automatisch zelf-toegevoegd wanneer ze worden gedefinieerd op hun maximaal toegelaten domein

\[\mathop{\mathrm{\mathcal{D}}}\,\!_{{\hat{X}}} = \{f \in H | \int_{-\infty}^{+\infty} {\left\lvert x f(x)\right\rvert}^2\,{\mathrm{d}}x < \infty\}\]

\[\mathop{\mathrm{\mathcal{D}}}_{{\hat{P}}} = \{f \in H | f'\ \text{bestaat en}\ \int_{-\infty}^{+\infty} {\left\lvert f'(x)\right\rvert}^2\,{\mathrm{d}}x < \infty\}\]

($f \in \mathop{\mathrm{\mathcal{D}}}_{{\hat{P}}}$ impliceert $\lim_{x\to \pm \infty} f(x) = 0$)

Spectraaltheorie

(geen bewijzen)

Eigenwaarden en eigenvectoren

Eigenwaarden van operatoren op oneindig-dimensionale Hilbertruimten:

Voorbeeld met momentumoperator: soms geen eigenwaarden, soms volledig ${\mathbb{C}}$ als eigenwaarde
Ander voorbeeld op $\ell^2({\mathbb{N}})$:

\[\begin{align} {\hat{A}}^- {e}_n &= \begin{cases} {o}, & n=0\\ \sqrt{n} {e}_{n-1},&n > 0 \end{cases}, &{\hat{A}}^+{e}_{n} = \sqrt{n+1} {e}_{n+1}. \end{align}\]
- ${v}= \sum_{n=0}^{+\infty} \frac{\lambda^n}{\sqrt{n!}} {\mathrm{e}}^{-{\left\lvert\lambda\right\rvert}^2/2} {e}_n$: ${\left\lVert{v}\right\rVert}_2 = 1$ en ${\hat{A}}^-{v}= \lambda {v}$ voor alle $\lambda \in {\mathbb{C}}$
- ${\hat{A}}^+ = ({\hat{A}}^{-})^\dagger$: geen eigenwaarden en eigenvectoren
Positie-operator ${\hat{X}}$ op $L^2([a,b])$: (begrensde operator!)
- geen exacte eigenvectoren (normaliseerbare functies in $L^2([a,b])$)
- $f_{\lambda,\epsilon}(x) = \begin{cases} \frac{1}{\sqrt{2\epsilon}},&{\left\lvert x-\lambda\right\rvert} < \epsilon\\ 0,&\text{elsewhere} \end{cases}$ voldoet aan ${\left\lVert x f(x) - \lambda f(x)\right\rVert}^2 = \int_{\lambda-\epsilon}^{\lambda+\epsilon} \frac{(x-\lambda)^2}{2\epsilon}\,{\mathrm{d}}x = \frac{\epsilon^2}{3}$ voor alle $\lambda \in [a,b]$

Compacte operatoren

compacte operatoren (deelverzameling van begrende operatoren)
- klasse van operatoren die zich meer als een “matrix” gedragen
- van belang voor de (theoretische) ontwikkeling van Greense functies etc
- technische definitie: ${\hat{A}}$ is compact als, voor elke begrensde rij $({v}_n \in H)_{n \in {\mathbb{N}}_0}$, $(w_n ={\hat{A}}{v}_n)_{n \in {\mathbb{N}}_0}$ een convergerende deelrij bevat
  
  (m.a.w.: begrensde deelverzameling $\stackrel{{\hat{A}}}{\longrightarrow}$ compacte deelverzameling)
- bevat de klasse van Hilbert-Schmidt operatoren:
  
  \[{\left\lVert{\hat{A}}\right\rVert}_{\text{HS}}^2 = \sum_{n =1}^{+\infty} {\left\lVert{\hat{A}}{e}_n\right\rVert}^2 < \infty\]
  
  of voor een integraaloperator
  
  \[{\left\lVert{\hat{A}}\right\rVert}_{\text{HS}}^2 = \int_I \int_I {\left\lvert A(x,y)\right\rvert}^2 \,{\mathrm{d}}x {\mathrm{d}}y < \infty\]

Compacte operatoren

zelftoegevoegde compacte operator ${\hat{A}}$ beschikt over een spectrale decompositie

\[{\hat{A}} = \sum_{n} \lambda_n {\hat{P}}_{\lambda_n}\quad \implies H = V_0 \bigoplus_{n} V_{\lambda_n}\]
- $\lambda_n \in {\mathbb{R}}$
- aantal eigenwaarden $\lambda_n \neq 0$ eindig of aftelbaar oneindig
- elke $V_{\lambda_n \neq 0}$ is eindig-dimensionaal, $V_0$ kan oneindig-dimensionaal zijn
- $(\lambda_n)$ kan gesorteerd worden zodat ${\left\lvert\lambda_n\right\rvert}$ niet-stijgend is (${\left\lvert\lambda_{n+1}\right\rvert} \leq {\left\lvert\lambda_n\right\rvert}$)
- ${\left\lvert\lambda_1\right\rvert} = {\left\lVert{\hat{A}}\right\rVert}$ (operatornorm)
- $\lim_{n\to \infty} \lambda_n =0$, of dus, aantal eigenwaarden met ${\left\lvert\lambda_n\right\rvert} > \epsilon$ is eindig

Compacte operatoren

algemene compacte operator ${\hat{A}}$ beschikt over Schmidt-decompositie:

niet-stijgende rij positieve getallen $(\sigma_n \in {\mathbb{R}}_{\geq 0})_{n \in {\mathbb{N}}_0}$ en verzamelingen orthonormale vectoren $(u_n \in H)_{n \in {\mathbb{N}}_0}$ en $(v_n \in H)_{n \in {\mathbb{N}}_0}$ met ${\hat{A}}u_n = \sigma_n v_n$ en ${\hat{A}}^\dagger v_n = \sigma_n u_n$ zodat

\[{\hat{A}} {w}= \sum_{n} \sigma_n {u}_n {\left\langle{v}_n,{w}\right\rangle}, \forall {w}\in H\]
- veralgemening van singuliere waardendecompositie
- van belang voor definitie van kwantumverstrengeling (“entanglement”)

Spectrum van algemene operatoren

Operator ${\hat{A}}$ met dicht domein $\mathop{\mathrm{\mathcal{D}}}_{{\hat{A}}}$ en bereik $\mathcal{R}_{{\hat{A}}}$ is injectief indien $\mathop{\mathrm{ker}}({\hat{A}})=\{{o}\}$

$\Rightarrow$ we kunnen de inverse ${\hat{A}}^{-1}$ definiëren als operator met domein $\mathcal{R}_{{\hat{A}}}$

$\Rightarrow$ deze inverse is enkel “dicht gedefinieerd” als $\overline{\mathcal{R}_{{\hat{A}}}} = H$
Voor ${\hat{A}}\in \mathop{\mathrm{End}}(H)$ definiëren we de resolvente verzameling als de verzameling van complexe getallen $\lambda$ waarvoor
1. de inverse van ${\hat{A}}-\lambda {\hat{1}}$ kan worden gedefinieerd: $\mathop{\mathrm{ker}}({\hat{A}}-\lambda {\hat{1}}) = \{{o}\}$
2. EN deze inverse $({\hat{A}}-\lambda{\hat{1}})^{-1}$ dicht gedefinieerd is
3. EN deze inverse $({\hat{A}}-\lambda{\hat{1}})^{-1}$ begrensd is (zodat de definitie ervan kan worden uitgebreid tot volledig $H$)
- De resolvente verzameling is een open deelverzameling van ${\mathbb{C}}$
- Het complement in ${\mathbb{C}}$ is het spectrum $\sigma_{{\hat{A}}}$ van ${\hat{A}}$, en is dus een gesloten deelverzameling van ${\mathbb{C}}$

Spectrum van algemene operatoren

spectrum $\sigma_{{\hat{A}}}$ bevat verschillende bijdragen:
- puntspectrum $\sigma^{(\text{p})}_{{\hat{A}}}$: $\lambda \in {\mathbb{C}}$ waarvoor $\mathop{\mathrm{nullity}}({\hat{A}}-\lambda {\hat{1}}) > 0$ (de inverse kan niet worden gedefinieerd); dit zijn de echte eigenwaarden en eigenvectoren
- continu spectrum $\sigma^{(\text{c})}_{{\hat{A}}}$: $\lambda \in {\mathbb{C}}$ waarvoor $({\hat{A}}-\lambda {\hat{1}})^{-1}$ onbegrensd is; bij deze waarden $\lambda$ kan een “benaderende” eigenvector gevonden waarden zodat ${\left\lVert{\hat{A}}{v}-\lambda{v}\right\rVert} < \epsilon$, $\forall \epsilon > 0$
- residueel spectrum $\sigma^{(\text{r})}_{{\hat{A}}}$: $\lambda \in {\mathbb{C}}$ waarvoor $({\hat{A}}-\lambda {\hat{1}})^{-1}$ niet dicht gedefinieerd is $\rightarrow$ zie verder
het gehele spectrum is nooit leeg, maar sommige van de afzonderlijke types spectrum kunnen leeg zijn
begrensde operatoren ${\hat{A}}$: ${\left\lvert\lambda\right\rvert} > {\left\lVert{\hat{A}}\right\rVert} \implies \lambda \not \in \sigma_{{\hat{A}}}$
voor willekeurige operatoren: (maar zie verderop voor zelftoegevoegd)
- puntspectrum is niet noodzakelijk discreet (eindig of aftelbaar)
- continu spectrum is niet noodzakelijk onaftelbaar

Spectrum van algemene operatoren: voorbeelden

${\hat{A}}^-$ op $\ell^2({\mathbb{N}})$: $\sigma^{(\text{p})}= {\mathbb{C}}$
${\hat{X}}$ op $L^2([a,b])$:
- $\mathop{\mathrm{ker}}({\hat{X}}-\lambda{\hat{1}}) = \{0\}$ voor alle $\lambda \in {\mathbb{C}}$ $\Rightarrow \sigma^{(\text{p})} = \emptyset$
- $\mathcal{R}_{{\hat{X}}-\lambda{\hat{1}}}$: steeds dichte deelruimte van $H$
  - kwadratisch integreerbare functies met $f(\lambda) = 0$ als $\lambda \in [a,b]$)
  - volledig $H$ als $\lambda \not\in[a,b]$
  $\Rightarrow \sigma^{(\text{p})} = \emptyset$
- $({\hat{X}}-\lambda)^{-1}$ werkt op $\mathcal{R}_{{\hat{X}}-\lambda{\hat{1}}}$: $f(x) \mapsto g(x) = (x-\lambda)^{-1} f(x)$
  - ${\left\lVert g\right\rVert} \leq (\max_{x}{\left\lvert x-\lambda\right\rvert}^{-1}) {\left\lVert f\right\rVert}$ als $\lambda \not \in [a,b]$
  - ${\left\lVert g\right\rVert}$ niet te begrensen door ${\left\lVert f\right\rVert}$ als $\lambda \in [a,b]$ $\Rightarrow$ $\sigma^{(\text{c})} = [a,b]$

Spectrum van algemene operatoren: voorbeelden

Op $H = \ell^2({\mathbb{N}}_0)$: operator ${\hat{A}}:e_n \mapsto \frac{1}{n}e_n$ voor alle $n \in {\mathbb{N}}_0$
- Elke $e_n$ is een eigenvector met eigenwaarde $\frac{1}{n}$: $\sigma^{(\text{p})} = \{n^{-1}; n \in {\mathbb{N}}_0\}$
- $({\hat{A}}-\lambda {\hat{1}})^{-1} \sum_{n\in{\mathbb{N}}_0} v^n {e}_n = \sum_{n\in{\mathbb{N}}_0} \frac{1}{n^{-1} - \lambda} v^n {e}_n$
  - $\lambda \not \in {\mathbb{N}}$: goed gedefinieerd en begrensd voor alle ${v}\in H$
  - $\lambda = 0$: gedefinieerd op $\{ {v}\in \ell^2({\mathbb{N}}_0) | \sum_{n\in{\mathbb{N}}_0} n^2 {\left\lvert v^n\right\rvert}^2 < \infty\}$ maar onbegrend: ${\left\lVert{\hat{A}}^{-1}{e}_n\right\rVert} = n {\left\lVert{e}_n\right\rVert} = n$
  $\Rightarrow \sigma^{(\text{c})} = \{0\}$

Spectrum van algemene operatoren: voorbeelden

Op $H = \ell^2({\mathbb{N}}_0)$: verschuivingsoperatoren

\[{\hat{L}} (v^0, v^1, v^2, \ldots) = (v^1, v^2, v^3, \ldots),\quad{\hat{R}} (v^0, v^1, v^2,\ldots) = (0, v^0, v^1, \ldots)\]
- ${\hat{L}}^\dagger = {\hat{R}}$ en vice versa, ${\left\lVert{\hat{L}}\right\rVert} = {\left\lVert{\hat{R}}\right\rVert}=1 \implies {\left\lvert\lambda\right\rvert} > 1$ niet in spectrum
- $\mathop{\mathrm{ker}}({\hat{R}} - \lambda {\hat{1}}) =\{0\}$ voor alle $\lambda$: $\sigma^{(\text{p})}_{{\hat{R}}} = \emptyset$
- ${v}_\lambda = \sum_{n=0}^{+\infty} \lambda^n {e}_n$ is eigenvector van ${\hat{L}}$ met eigenwaarde $\lambda$: ${v}_\lambda$ is normaliseerbaar voor ${\left\lvert\lambda\right\rvert}<1$ $\Rightarrow$ $\sigma^{(\text{p})}_{{\hat{L}}} = \{\lambda \in {\mathbb{C}}| {\left\lvert\lambda\right\rvert}< 1\}$
- m.b.v. $\mathop{\mathrm{im}}({\hat{R}}-\lambda {\hat{1}})^\perp = \mathop{\mathrm{ker}}(({\hat{R}}-\lambda {\hat{1}})^\dagger) = \mathop{\mathrm{ker}}({\hat{L}}-{\overline{\lambda}}{\hat{1}})$
  
  $\implies \mathop{\mathrm{im}}({\hat{R}}-\lambda {\hat{1}})^{\perp\perp} = \overline{\mathop{\mathrm{im}}({\hat{R}}-\lambda {\hat{1}})} = \mathop{\mathrm{ker}}({\hat{L}} - \overline{\lambda}{\hat{1}})^\perp$
  
  $\implies ({\hat{R}}-\lambda {\hat{1}})^{-1}$ niet dicht gedefinieerd als ${\overline{\lambda}}$ eigenwaarde is van ${\hat{R}}^\dagger = {\hat{L}}$ $\implies \sigma_{{\hat{R}}}^{(\text{r})} = \{\lambda \in {\mathbb{C}}| {\left\lvert\lambda\right\rvert}< 1\}$

Spectrum van algemene operatoren: voorbeelden

Op $H = \ell^2({\mathbb{N}}_0)$: verschuivingsoperatoren

\[{\hat{L}} (v^0, v^1, v^2, \ldots) = (v^1, v^2, v^3, \ldots),\quad{\hat{R}} (v^0, v^1, v^2,\ldots) = (0, v^0, v^1, \ldots)\]
- $\sigma_{{\hat{L}}}^{(\text{c})} = \sigma_{{\hat{R}}}^{(\text{c})} = \{\lambda \in {\mathbb{C}}| {\left\lvert\lambda\right\rvert}= 1\}$: benaderende eigenvectoren
  - ${v}_{\lambda,n} = \frac{1}{\sqrt{n}} \sum_{k=0}^{n-1} {\mathrm{e}}^{{\mathrm{i}}k\phi} {e}_k$ met $\lambda = {\mathrm{e}}^{{\mathrm{i}}\phi}$:
    
    ${\left\lVert{\hat{L}} {v}_{\lambda,n} - \lambda {v}_{\lambda,n}\right\rVert} = {\left\lVert\frac{1}{\sqrt{n}} {\mathrm{e}}^{{\mathrm{i}}\phi n} {e}_{n-1}\right\rVert} = \frac{1}{\sqrt{n}}$
  - ${v}'_{\lambda,n} = \frac{1}{\sqrt{n}} \sum_{k=0}^{n-1} {\mathrm{e}}^{-{\mathrm{i}}k\phi} {e}_k$ met $\lambda = {\mathrm{e}}^{{\mathrm{i}}\phi}$
    
    ${\left\lVert{\hat{R}} {v}'_{\lambda,n} - \lambda {v}'_{\lambda,n}\right\rVert} = {\left\lVert\frac{1}{\sqrt{n}} {\mathrm{e}}^{-{\mathrm{i}}\phi (n-1)}{e}_{n} - \frac{1}{\sqrt{n}} {\mathrm{e}}^{{\mathrm{i}}\phi } {e}_{0}\right\rVert} = \sqrt{\frac{2}{n}}$

Spectrum van zelftoegevoegde operatoren

Voor een zelftoegevoegde operator ${\hat{A}}={\hat{A}}^\dagger$ geldt:
- $\sigma \subseteq {\mathbb{R}}$
- $\sigma^{(\text{r})} = \emptyset$
- $\sigma^{(\text{p})}$ is discreet: eindig of aftelbaar (want bijbehorende eigenvectoren vormen orthonormale rij: moet aftelbaar zijn)
$\Rightarrow$ er kan een soort spectrale decompositie worden opgeschreven die zowel het puntspectrum als het continue spectrum omvat

$\Rightarrow$ in de fysica schrijven we dit met “eigenvectoren” met een “Dirac-delta normalisering”

Doel van dit hoofdstuk

Doel van dit hoofdstuk

Functieruimten en normen

Functieruimten

Lebesgue-ruimten

Lebesgue-ruimten

Van seminorm naar norm

Van seminorm naar norm

Lebesgue-integraal

Lebesgue-integraal

Lebesgue-integraal

“Bijna overal” en “maat nul” (nulverzamelingen)

Compleetheid van \(L^p(I;{\mathbb{F}})\)

Bijkomende opmeringen

Hilbertruimten en inwendig product

Hilbertruimten en inwendig product

Orthogonale veeltermen

Orthogonale veeltermen

Orthogonale veeltermen

Orthogonale veeltermen

Orthogonale veeltermen: Legendre

Orthogonale veeltermen: Hermite

Orthogonale veeltermen: Laguerre

Orthogonale veeltermen: Chebyshev

Toepassing: Gaussische kwadratuur

Toepassing: Gaussische kwadratuur

Fourierreeksen

Periodieke functies

Trigonometrische veeltermen en Fouriercoefficiënten

Fouriercoefficiënten: eigenschappen

Convoluties

Convergentie (geen stellingen/bewijzen)

Gladheid en convergentiesnelheid

Convoluties herbekeken

Stuksgewijze continuïteit en Gibbsfenoneem

Stuksgewijze continuïteit en Gibbsfenoneem

Relatie met discrete Fouriertransformatie

Operatoren op Hilbertruimten

Veelvoorkomende operatoren op functieruimten

Veelvoorkomende operatoren op functieruimten

Domein van een operator

Domein van een operator

Begrensde en onbegrensde operatoren

Begrensde en onbegrensde operatoren

Begrensde en onbegrensde operatoren

Toegevoegde van een onbegrensde operator

Toegevoegde: eigenschappen en voorbeelden

Symmetrische en zelftoegevoegde operatoren

Uitgebreid voorbeeld

Uitgebreid voorbeeld

Uitgebreid voorbeeld

Positie- en momentumoperator op \(L^2({\mathbb{R}})\)

Spectraaltheorie

Eigenwaarden en eigenvectoren

Compacte operatoren

Compacte operatoren

Compacte operatoren

Spectrum van algemene operatoren

Spectrum van algemene operatoren

Spectrum van algemene operatoren: voorbeelden

Spectrum van algemene operatoren: voorbeelden

Spectrum van algemene operatoren: voorbeelden

Spectrum van algemene operatoren: voorbeelden

Spectrum van zelftoegevoegde operatoren